Wybory powinny być równe, a więc głos każdego obywatela powinien mieć taką samą wagę. To co możemy już powiedzieć na temat wyborów parlamentarnych w roku 2023 to to, że równe nie będą.
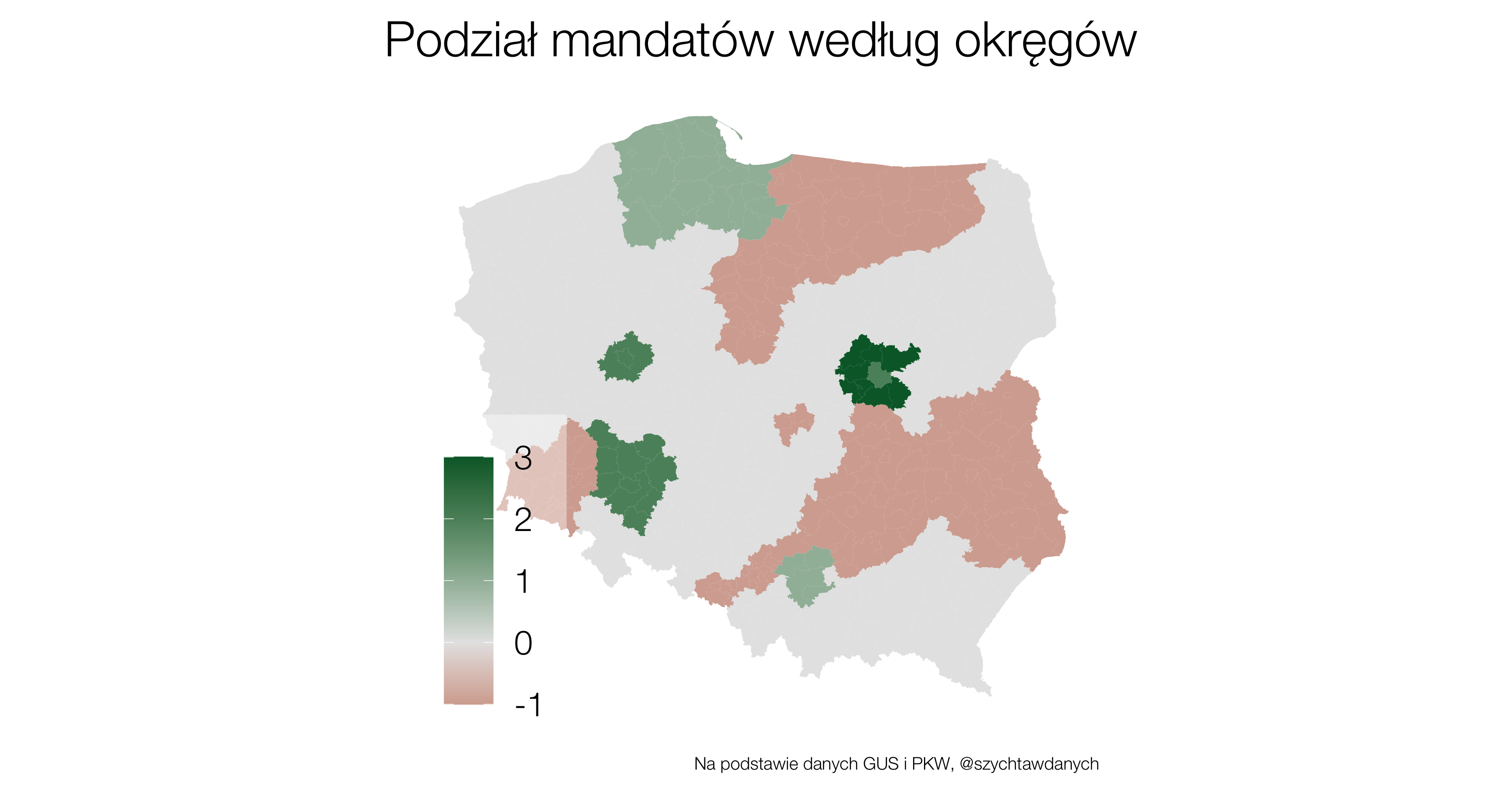
Wybory powinny być równe, a więc głos każdego obywatela powinien mieć taką samą wagę. To co możemy już powiedzieć na temat wyborów parlamentarnych w roku 2023 to to, że równe nie będą.

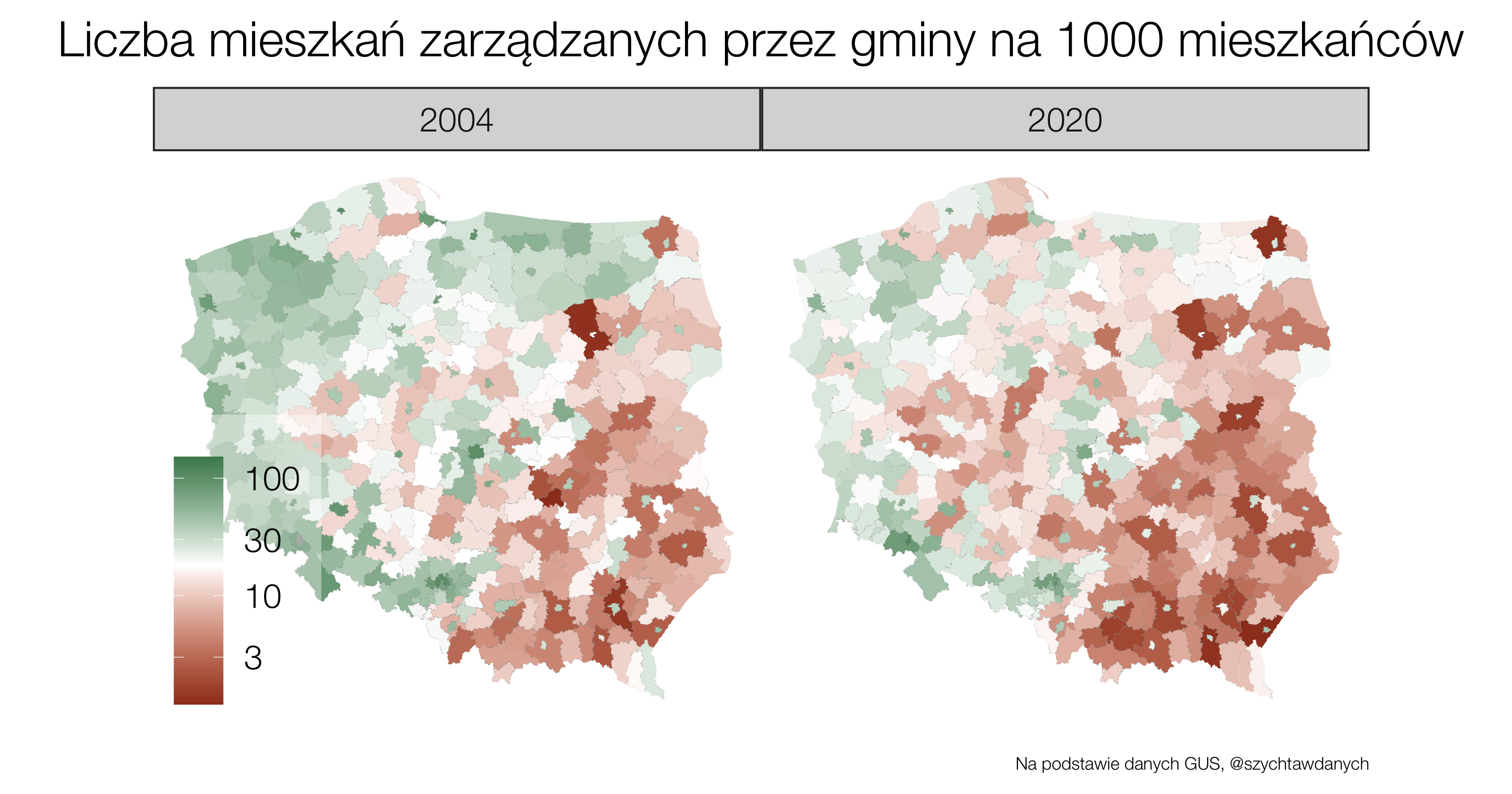
Jak zmienia się liczba mieszkań należących do gmin? Czy są regiony gdzie budownictwo społeczne cieszy się większym zainteresowaniem? I jak te fakty mają się do konstytucyjnej zasady sprawiedliwości społecznej?