O wynikach ostatnich wyborów
Rozkłady poparcia dla partii w komisjach obwodowych, czyli poparcie w pojedynczych lokalach wyborczych, nie mają rozkładu normalnego i mają różny kształt w zależność od partii. Przynajmniej w Polsce. Oznacza to nie tylko, że partie cieszą się różną skalą poparcia społecznego, ale też, że niektóre partie wzbudzają bardziej skrajne odczucia wyborców niż inne, tj. albo ich poparcie jest bardzo wysokie, albo bardzo niskie.
W dzisiejszym poście postaram się odpowiedzieć na pytania: Czy jeśli pogrupujemy wyniki z komisji obwodowych względem województw to ,,odzyskamy" normalność? Czy rozkłady poparcia dla jednej partii w różnych województwach są podobne? I czy powinny one być podobne?
Na wstępie, muszę sprostować swój poprzedni wpis i zwrócić część honoru Państwowej Komisji Wyborczej. Okazało się, że dane za ostatnie wybory są jednak dostępne (choć nieco ukryte). Nie wiem czy było to moje przeoczenie, czy też pojawiły się tam one w międzyczasie. Dlaczego tylko część honoru? Bo opublikowane wyniki nie są kompletne. Jeśli chodzi o dane dotyczące wyborów do sejmików wojewódzkich to brakuje danych m.in. danych dla Wałbrzycha czy większości komisji w Warszawie. Mimo wszystko dane są dosyć wiarogodne - pochodzą z niemal 26,500 komisji na istniejących 27,500. Nawet prosty histogram, skonstruowany na ich podstawie, jest interesujący i pokazuje zasadniczą różne struktury poparcia dla wszystkich czterech największych partii.

Rozkłady poparcie dla partii w województwach zależą nie tylko od partii, ale i od województwa. Dlaczego wydaje mi się to nietrywialnym stwierdzeniem? Dlatego, że chociaż poparcie w województwach dla konkretnej partii może być różne (wszak mamy mieszankę wyników z bardzo różnych terenów, z różnymi kandydatami i komitetami), to rozkład w obrębie jednego województwa powinien być w miarę ,,spójny". Tyle moja intuicja, która okazała się całkowicie błędna, a teraz wykresy:


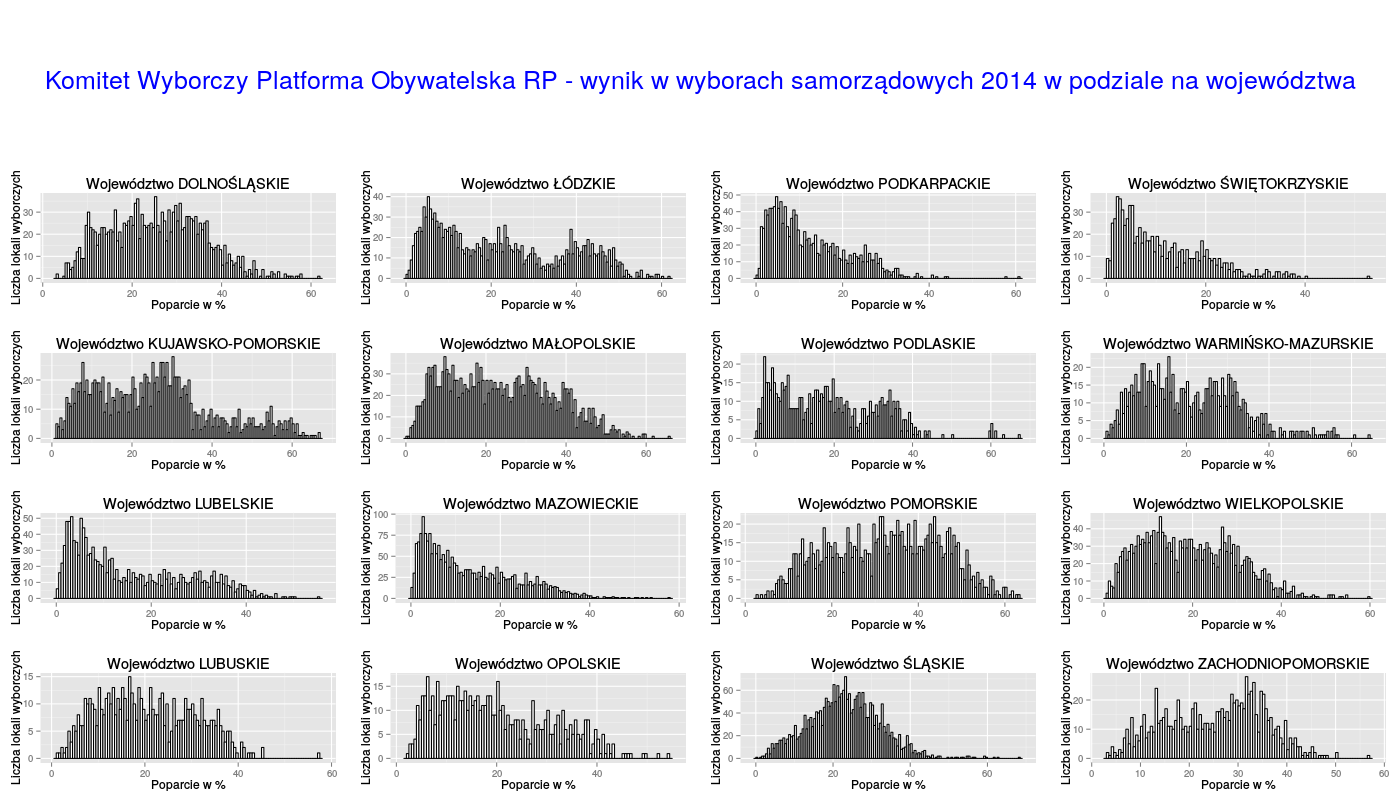

Skrypty można znaleźć, podobnie jak poprzednio, na githubie.
Za kilka dni pojawią się kolejne wpisy z bardziej wysublimowanymi analizami.